Kombinatorik

Kombinatorik ist ein Teilgebiet der Stochastik, das sich mit dem systematischen Zählen von Möglichkeiten befasst, also der Anzahl, wie Objekte angeordnet (Permutation) oder ausgewählt (Kombination, Variation) werden können, unter Berücksichtigung von Reihenfolge und Wiederholung.

Es werden drei verschiedene Abzählmethoden unterschieden:

Variation – Stichprobe mit Berücksichtigung der Reihenfolge

Eine Auswahl von k Objekten aus einer Menge von n Objekten in einer bestimmten Reihenfolge. Können Objekte dabei mehrfach ausgewählt werden, so spricht man von einer Variation mit Wiederholung, darf jedes Objekt nur einmal auftreten, von einer Variation ohne Wiederholung.

Kombination – ungeordnete Stichprobe

Eine Auswahl von k Objekten aus einer Menge von n Objekten. Die Reihenfolge spielt keine Rolle. Können Objekte dabei mehrfach ausgewählt werden, so spricht man von einer Kombination mit Wiederholung, darf jedes Objekt nur einmal auftreten, von einer Kombination ohne Wiederholung.

Permutation

Eine Anordnung von n Objekten in einer bestimmten Reihenfolge. Je nachdem, ob manche Objekte mehrfach auftreten dürfen oder nicht, spricht man von einer Permutation mit Wiederholung oder einer Permutation ohne Wiederholung.

Fragen zur Abzählmethode

– Werden alle n Elemente aus einer Menge mit n Objekten genutzt, oder nur eine Auswahl k?
– Ist die Reihenfolge von Bedeutung oder nicht?
– Darf ein Element mehrfach vorkommen oder nicht?

Links

Farbkombinationen
Es kann ein Bild hochgeladen und Farben definiert werden.
Das Tool gibt die Kombinationen und Variationen als Bilder aus.

Variation ohne Wiederholung

Im Vergleich zur Variation mit Wiederholung ist es hier für jedes nachfolgende Objekt nicht mehr möglich, ebenso n Elemente auszuwählen.

Wähle k Elemente aus n mit Reihenfolge ohne Zurücklegen

Als Variation ohne Wiederholung wird in der Kombinatorik eine Stichprobe genannt, bei der k aus n Objekten ausgewählt werden, wobei die Reihenfolge entscheidend ist und Objekte nur einmal gewählt werden dürfen.

Für die Berechnung ist also eine Angabe von k und n Objekten entscheidend. Wichtig ist, wie in der Definition erwähnt, dass nur eine Auswahl verwendet wird und nicht die komplette Menge an Objekten. Ansonsten würde es sich um eine Permutation handeln.

Formel:

n!
–––––––
(n – k)!

Das bedeutet, dass für das erste Objekt, das gewählt wird, n Möglichkeiten bestehen. Wird das Objekt nicht mehr in die Auswahlmenge zurückgelegt, gibt es für den nächsten Schritt...

(n – 1)

Möglichkeiten. Das ist deshalb der Fall, weil keine Wiederholung stattfindet. Eine Farbe darf nur einmal vorkommen und steht nicht mehr zur Auswahl.

Das geht weiter bis

(n – k + 1)

da nicht die ganze Farbpalette betrachtet werden, sondern nur eine Auswahl, gilt

(n – 1) x (n – 2) ... x 1 = n!

Für die schlussendliche Formel werden also alle Möglichkeiten, verwendet, die es geben würde, wenn die gesamte Farbpalette verwendet würde und diese werden durch die tatsächliche Anzahl geteilt.

Beispiele

Quadcolor Tartan
Die Gesamtmenge an an Farbkombinationen und Anordnungen der Farben
n = Farbpalette
k = Anzahl Farben im Design, hier 4

Variation mit Wiederholung

Als Variation wird in der Kombinatorik eine geordnete Stichprobe für die Auswahl von Objekten in einer festen Reihenfolge bezeichnet.

Somit werden bei einer Variation mit Wiederholung k aus n Objekten unter Beachtung der Reihenfolge ausgewählt. Die Objekte können hierbei mehrmals ausgewählt werden.

1. Alle Elemente n aus der angegebenen Menge sind unterscheidbar. So haben Kugeln unterschiedliche Zahlen oder verschiedene Schülerinnen oder Schüler sind im Experiment gegeben.

2. k Elemente werden ausgewählt.

3. Die Reihenfolge ist entscheidend. Für eine vierstellige PIN ist unbedingt die Reihenfolge der Zahlen ausschlaggebend.

4. Elemente sind mehrfach wählbar. Deine PIN am Smartphone oder am Fahrradschloss darf 0000 heißen.

Wähle k Elemente aus n mit Reihenfolge mit Zurücklegen

Beispiel: Eine PIN mit vier Zahlen

Zur Berechnung von Aufgaben mit einer Variation mit Wiederholung benötigst Du die folgende Formel:

N hoch k

wobei n für die Anzahl der Ausgangsmenge steht und k für die ausgewählten Elemente

Erklären lässt sich dieser Zusammenhang wieder sehr anschaulich mit den Kugeln aus dem Urnenmodell. Überlege Dir dabei, welche Bedingungen gelten: Du möchtest aus n Objekten k auswählen, wobei die Reihenfolge wichtig ist und mit Wiederholung (also mit Zurücklegen).

Für das erste Objekt hast Du n Möglichkeiten. Da Objekte wieder mehrfach gewählt werden dürfen, bzw. Du Kugeln in die Urne zurücklegen darfst, hast Du für das zweite Objekt auch n Möglichkeiten und für das k-te Objekt ebenso.

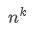
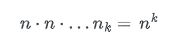
Beispiel

?

Kombination ohne Wiederholung

Wähle k Elemente aus n ohne Reihenfolge ohne Zurücklegen.

Die Formel für eine Variation ohne Wiederholung ist:

\frac{n!}{(n - k)!}

Da bei der Kombination ohne Wiederholung die verschiedenen Anordnungen keine Rolle spielen, wird das Ergebnis nochmals durch k! geteilt:

\frac{n!}{(n - k)! \cdot k!}

Dies nennt man auch Binomialkoeffizient und wird wie folgt geschrieben:

(\binom{n}{k})

Alle 10 Kombinationen ohne Wiederholung von 3 aus 5 Objekten

5 × 4 × 3 × 2 × 1 120

––––––––––––––––– = ––––– = 10

2 × 3 × 2 × 1 12

Beispiele Kombination ohne Wiederholung

k = Anzahl verwendete Farben
n = Anzahl zur Verfügung stehende Farben / Farbpalette

Dreifarbiger Interlock

Duotones: zweifarbiger Schlauchjacquard (Vor- und Rückseite gleich, deshalb Position egal)

Hue Beanie Mouliné (zwei verschiedenfarbige Fäden)

Kombination mit Wiederholung

Bei einer Kombination mit Wiederholung werden k aus n Objekten aus der Menge gewählt, wobei die Reihenfolge nicht beachtet wird. Objekte können dabei mehrfach ausgewählt werden.

Formel

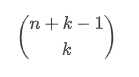
(n + k – 1)!
––––––––––––
(n – 1)! × k!

Die einzelnen Teile erklärt:
(n + k – 1)!
Die n möglichen Kombinationen werden um k – 1 erhöht, da für den Fall k = 1 die Kombination mit und ohne Wiederholung keinen Unterschied ergibt.

(n – 1)!
Keine Berücksichtigung weiterer Kombinationen: Es wird ein Objekt entnommen, also befinden sich noch n – 1 Objekte in der Gesamtmenge, was allerdings für diesen Fall unwichtig ist

k!
Ohne Reihenfolge: Die Formel für die Kombination mit Wiederholung wird für k! um die Objekte reduziert, die zu einer unterschiedlichen Reihenfolge führen würden. Dabei werden also die Kombination von Farben wie Mauve / Wassermelone und Wassermelone / Mauve als eine Kombination gewertet

Beispiele:

k = Anzahl verwendete Farben
n = Anzahl zur Verfügung stehende Farben / Farbpalette

Mouliné und Solid Rib Tartan 3ply
wenn alle Möglichkeiten gezählt werden, die mit drei Fäden gestrickt werden
– alle drei Fäden in der gleichen Farbe (=n)
plus
– alle drei Fäden in unterschiedlicher Farbe (= Kombination ohne Wiederholung)
plus
– zwei gleichfarbige und ein unterschiedlicher Faden

Permutation ohne Wiederholung

Eine Permutation ohne Wiederholung ist eine Anordnung von n Objekten, die alle unterscheidbar sind. Nachdem es für das erste Objekt n Platzierungsmöglichkeiten gibt, kommen für das zweite Objekt nur noch n−1 Möglichkeiten in Betracht, für das dritte Objekt nur mehr n−2 und so weiter bis zum letzten Objekt, dem nur noch ein freier Platz bleibt. Die Anzahl der möglichen Permutationen von n Objekten wird demnach durch die Fakultät angegeben. (Text Wikipedia)

n! genannt n Fakultät

Formel

n! = n \cdot (n - 1) \cdot (n - 2) \cdot \dots \cdot 1

Beispiel Wikipedia:
4! = 4 × 3 × 2 × 1 = 24 mögliche Anordnungen von vier verschiedenfarbigen Kugeln in einer Reihe.

Beispiele Permutation ohne Wiederholung

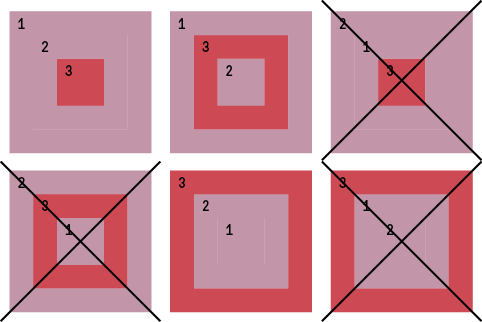
Die Auswahl der Farben hat bereits stattgefunden. Wieviele mögliche Anordnungen gibt es in einem Muster?
Interessant bei Mustern, die nicht gleichmässig sind.

– Quadcolor Tartan
Es wurden vier Farben gewählt. Wieviele Möglichkeiten der Anordnung im Muster gibt es?

4! = 4 \cdot 3 \cdot 2 \cdot 1 = 24

Das entspricht dem Wikipedia-Beispiel mit den vier Kugeln.

– Dreifarbiger Jacquard oder dreifarbiges Intarsia-Muster
Die drei Farben sind fix. Wieviele Möglichkeiten der Anordnung im Muster gibt es?

3! = 3 \cdot 2 \cdot 1 = 6

Sechs Quadrate mit je drei Farben in unterschiedlicher Anordnung — Farbe 1 = Mauve
Farbe 2 = Blau
Farbe 3 = Wassermelone

Weiteres Beispiel mit gleicher Anzahl Möglichkeiten:
Die Fadenführerfolgen beim Stricken mit drei (n) Systemen / Fadenführern:

1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1

Permutation mit Wiederholung

Eine Permutation mit Wiederholung ist eine Anordnung von n Objekten, von denen manche nicht unterscheidbar sind. Sind genau k Objekte identisch, dann sind diese auf ihren Plätzen vertauschbar, ohne dass sich dabei eine neue Reihenfolge ergibt. Auf diese Weise sind genau k! Anordnungen gleich. Die Anzahl der Permutationen von n Objekten, von denen k identisch sind, ist demnach durch die (n−k)-te fallende Faktorielle gegeben. (Text Wikipedia)

Formel

\frac{n!}{k!} = n \cdot (n - 1) \cdot \dots \cdot (k + 1) = n^{_n - k}

Gibt es nicht nur eine, sondern s Gruppen mit jeweils k1,…,ks identischen Objekten, so können all diese Objekte auf ihren Plätzen vertauscht werden, ohne dass sich neue Anordnungen ergeben. Zählt man auch die Objekte, die nur einmal vorkommen, mit Vielfachheit 1, dann gilt k1+…+ks=n und die Anzahl der möglichen Permutationen wird durch den Multinomialkoeffizienten angeben. (Text Wikipedia)

Formel

\frac{n!}{k_{1}! \cdot \dots \cdot k_{s}!} = (n, k_{1}, \dots, k_{s})

Beispiele Permutation mit Wiederholung

Triotones
Diese sind eigentlich vierteilig aufgebaut mit abwechselnd jeweils 2 Farben / Fadenführern pro Durchgang, eine der Farben kommt jedoch in jedem Durchgang vor.

Wenn die Farben bereits gewählt sind berechnet man mittels Multinomialkoeffizienten die möglichen Anordnungen dieser Farben.

n = 4 k = 2 4 x 3 x 2 x 1 = 24 geteilt durch 2 x 1 = 12

Überprüfen ob dies stimmt wenn man die Rückseite berücksichtigt

Das Beispiel bei der Permutation ohne Wiederholung, aber die Farbe Mauve kommt zweimal vor und Blau dafür nicht (oder vier Plätze)

3 x 2 x 1 / 2 x 1 = 3

Farbe 1 = Mauve
Farbe 2 = Mauve
Farbe 3 = Wassermelone

Grids unter die Beispiele nehmen